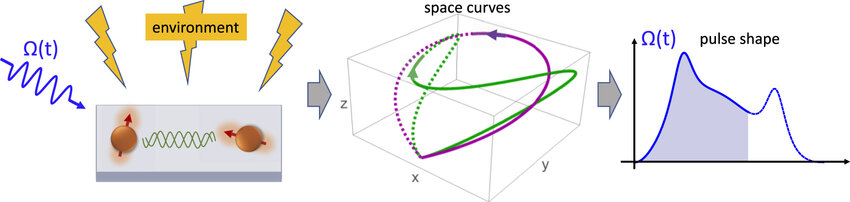
There is a subtle problem in quantum computing, that there is more than one way to realize the same quantum gate. Many different physical processes can realize the same transformation on the state of a qubit. So the question arises, which way is best? Due to the noisy nature of quantum computers, usually, the best way is one which is robust to the noise. The "Space Curve Quantum Control (SCQC) Formalism" is an approach to finding these "best" choices.
In particular, it lets us translate a quantum gate to a curve in 3d space (thus, a space curve). This translation makes previously hard to quantify "robustness properties" into nice geometric quantities. So we can use tools from fields like differential geometry and calculus to find curves which satisfy these geometric properties. Then we translate them back into quantum gates which are robust to noise. Within the SCQC formalism we are working on gates in sequence and feasibility. The past work only looks at one quantum gate at a time. It raised the question if there are better ways to use SCQC when you have multiple gates? Additionally, the current work produces very robust gates, but doesn't always give an evolution which is possible to run on current quantum computers. So we are studying what feasible gates look like under the transformation to a space curve and how to build robust yet feasible gates using the SCQC formalism.